What Is? 

Variational Two-Electron Reduced Density Matrix Theory (v2RDM) is a computational method in many-electron quantum mechanics wherein the electronic structure of a many-electron system is recovered from computation of the two-electron reduced density matrix. The underlying assumption of Hartree-Fock theory; that electrons are statistically independent (uncorrelated) means that it is insufficient for accurately describing the properties and behaviors of many chemical systems. V2RDM is unique amongst other post Hartree-Fock theories in that, rather than attempting to approximate the many-electron wavefunction, it instead capitalizes on the fact that the ground state energy of a many electron system is an exact functional of the 2-RDM. This is due to the fact that electrons are indistinguishable and have only pairwise interactions. To be able to use the 2-RDM to represent a many electron system, the 2-RDM had to be "constrained" into a form that could be accurately derived from the N-particle wavefunction. These constraints are known as the "N-representability conditions". In the limit that these constraints are properly applied, variational calculation of the 2-RDM allows for the very accurate modeling of strong electron correlation. 

History 

The concept of the density matrix in quantum mechanics was developed independently by both John von Neumann and Lev Landau in 1927, but until the late 1990s its application to electronic structure theory was superseded by self-consistent field (SCF) approaches such as Hartree-Fock and density functional theory. The reduced density operator was introduced by Paul Dirac in the 1930s, but it was not until 1951 that mathematician John Coleman first realized that the ground state energy of an N-electron system could be accurately represented via the "second order reduced density matrix", which is the 2-RDM. Coleman then coined the term "N-representability conditions" to describe the constraints that would need to be in place in order to calculate the ground state energy accurately from the 2-RDM.
The search for these conditions became known as the "N-representability problem". The N-representability problem inspired a great deal of collaboration throughout the mid 20th century, with a series of conferences bringing together chemists, physicists, and mathematicians working to inch towards N-representability. Claude Garrod and Jerome Percus were able to formally define the N-representability conditions in 1964, but application of these conditions to systems larger than four electrons was limited due to insufficient computational capabilities.
Advancements in the 1990s by Carmela Valdemoro, Hiroshi Nakatsuji, and David Mazziotti (and their respective collaborators) allowed for the calculation of the 2-RDM via the "contracted Schrodinger Equation" (CSE), which is the matrix representation of the Schrodinger equation "contracted" into the 2-electron space. Finally, in the early 2000s, Mazziotti, Erdahl, Nakatsuji, and others introduced an algorithm which allowed for the minimization of the ground state energy with respect to the 2-RDM via the semidefinite programming method.
 

Details 

In the density matrix formulation, the N-electron Schrodinger equation can be written as 

= E_n 

Where the N-electron density matrix is defined as 

Integrating this N-electron density matrix over electrons 3-N gives the 2-RDM 

The elements of the 2-RDM are obtained from taking the expectation value of Ψ with respect to the 2-electron reduced density operator (expressed here in second quantization), 

The energy of the system can then be expressed as a linear functional of the 2-RDM (where is the matrix representation of the 2-electron reduced Hamiltonian): 

To constrain the 2-RDM via the N-representability conditions two further 2-body RDMs; the particle-hole RDM and the hole-hole RDM are also defined: 

where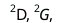and are all constrained to be positive semidefinite (Hermitian, and with no negative eigenvalues). The constraints that these three RDMs must be positive-semidefinite are known as the 2-positivity conditions, and are necessary constraints for allowing the 2-RDM to be derived from the N-particle wavefunctions.   

The energy of the system can then be variationally minimized while the linear functional is subject to constraints as per the N-representability conditions described above. This method of optimization is known as "semidefinite programming".  In particular, optimization is carried out via optimization algorithms similar to the method of Lagrange multipliers.  

Example 

As an example, the variational2RDM method, implemented in the Quantum Chemistry Toolbox in Maple, is applied to carbon dioxide in order to compute the total energy, correlation energy, and dipole moment.  

First, we load the quantum chemistry package and define the geometry of carbon dioxide via the location of its atoms in Cartesian coordinates.  

>

 

(4.1)

 

>

 

(4.2)

 

Plotting the molecule in 3D allows us to see that we have indeed correctly defined carbon dioxide. 

>

 

We can now carry out a v2RDM calculation to compute the ground state energy of carbon dioxide via the 2-RDM, as described above. We use the finite basis set STO-3g, which consists of three Gaussian orbitals used to approximate a single Slater-type orbital (STO). We have not specified an active space, and so the default active space for an even number of electrons, [2,2] (two electrons in two orbitals considered active for correlation) is used. This command returns a table containing information about the electronic structure. 

>

 

(4.3)

 

From this table we can extract the total ground state energy of carbon dioxide from v2RDM. 

>

 

(4.4)

 

We can also extract the correlation energy, which is the difference between the v2RDM ground state energy and the Hartree-Fock ground state energy, caused by the inclusion of electronic correlation in v2RDM. 

>

 

(4.5)

 

To see if we have fully captured the possible correlation in our molecule, we can expand the active space to include more active electrons and orbitals. 

>

 

(4.6)

 

>

 

(4.7)

 

Here we see an increase in our correlation energy, suggesting that the electronic correlation was not fully captured by limiting our active space to two electrons in two orbitals. 

Expanding our active space to include all 16 valence electrons in the system, we get: 

>

 

(4.8)

 

>

 

(4.9)

 

It is important to note that an active space comprised of all electrons and orbitals in the system would be prohibitively computationally expensive for larger systems. 

We can also see the specific molecular orbitals active for correlation. 

>

 

(4.10)

 

This output tells us that all but the three lowest energy MOs are active for electronic correlation. 

>

 

Selected References 

1. Quantum Mechanics of Many-Electron Systems. Proc. R. Soc. Lond. A 1929, 123 (792), 714–733.  

2. Coleman, A. J. Structure of Fermion Density Matrices. Rev. Mod. Phys. 1963, 35 (3), 668–686.  

3. Reduced-Density-Matrix Mechanics: With Application to Many-Electron Atoms and Molecules: Mazziotti/Advances Chem Physics V134; Mazziotti, D. A., Ed.; Advances in Chemical Physics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007.  

4. Colmenero, F.; Valdemoro, C. Approximating q -Order Reduced Density Matrices in Terms of the Lower-Order Ones. II. Applications. Phys. Rev. A 1993, 47 (2), 979–985.  

5. Yasuda, K.; Nakatsuji, H. Direct Determination of the Quantum-Mechanical Density Matrix Using the Density Equation. II. Phys. Rev. A 1997, 56 (4), 2648–2657.  

6. Mazziotti, D. A. Two-Electron Reduced Density Matrix as the Basic Variable in Many-Electron Quantum Chemistry and Physics. Chem. Rev. 2012, 112 (1), 244–262.