What Is ... Hartree-Fock Method?
Copyright (c) WhatIsProject 2023
What Is?
The Hartree-Fock method is an approximation to the many-electron Schrödinger equation in which the many-electron wave function is an antisymmetrized product of orbitals. Minimizing the energy with respect to this wave function yields an energetically optimal set of orbitals known as the Hartree-Fock molecular orbitals. Because of the wave function's orbital-product form, the many-electron Hamiltonian can be represented by an effective one-electron Hamiltonian in which the two-electron Coulomb repulsion terms are replaced with a mean-field repulsion in which a single electron experiences the average repulsion of the remaining electrons. While the average repulsion and the effective Hamiltonian depend on the Hartree-Fock orbitals, the Hartree-Fock orbitals and their energies can be computed from an iterative solution of the effective one-electron Hamiltonian until convergence, known as the self-consistent-field (SCF) method. Because of the antisymmetrized product wave function, the electrons of the Hartree-Fock method are described as uncorrelated. Improvement of the molecular energies and properties predicted from the Hartree-Fock method requires the solution of the Schrödinger equation with more accurate wave functions, known as correlated wave functions.
History
After working on anti-aircraft ballistics during World War I, Daniel Hartree pursued a Ph.D. under the guidance of Ernest Rutherford on Bohr's theory of the atom. In 1927, a year after completing his Ph.D., he proposed a self-consistent-field method (SCF) for approximately solving the Schrödinger equation for atoms and molecules. The technique, which became known as Hartree's method, aimed to solve the many-electron Schrödinger equation from first principles (ab initio) without empirical approximations. Contemporaries, however, did not fully understand the connection between Hartree's method and the many-electron Schrödinger equation. In 1928 John C. Slater (as well as J. A. Gaunt in an independent paper) showed that Hartree's method could be rigorously derived from the many-electron Schrödinger equation by assuming an orbital product for the wave function. Although Heisenberg and Dirac had shown in 1926 that the wave function for electrons must be antisymmetric upon particle exchange, Hartree's method did not produce an antisymmetrized wave function. In 1930 John C. Slater and Vladimir Fock independently showed that a more general method, which became known as the Hartree-Fock method, could be developed in which the orbital product was antisymmetrized. The antisymmetrization of the orbitals was accomplished by using a determinant, first employed by Heisenberg and Dirac in their 1926 paper, which became known as a Slater determinant. A workable self-consistent-field theory for solving the Hartree-Fock method was introduced in a paper written in 1935 by Daniel Hartree and his engineer father William Hartree. An efficient procedure for solving the Hartree-Fock equations on a digital computer was introduced in 1951 by Clemens Roothan, who had been a Ph.D. student with Robert Mulliken.
Details
The Hartree-Fock method approximates the solution of the non-relativistic N-electron Schrödinger equation

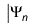
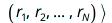 = En
= En 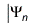

in which Zk is the proton number of the kth atom and the mass μ and Planck's constant ℏ are equal to 1 in atomic units. The wave function is approximated as an antisymmetrized product of orbitals, the Slater determinant
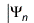

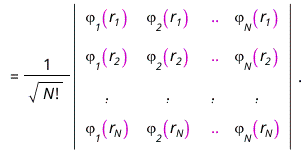
The orbital-product form of the wave function allows us to determine the orbitals and their energies εn from the self-consistent solution of an effective one-electron Schrödinger equation
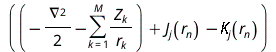
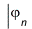
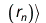 = εn
= εn 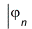

The effective one-electron Hamiltonian in the above equation is known as the Fock operator in honor of Vladimir Fock while the J and K, known as the Coulomb and exchange terms, represent the mean-field approximation of the electron-electron Coulomb repulsion. Formally, we can express the J and K terms as follows:
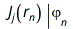
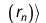
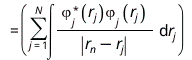
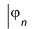

and
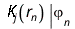
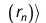

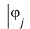
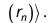
The Coulomb term arises in Hartree's method from the product of orbitals, but the exchange term is purely a consequence of the antisymmetry of the wave function.
The Hartree-Fock equations are solved by a self-consistent-field (SCF) procedure. In the SCF procedure the orbitals are updated through an iterative solution. The main steps of the SCF procedure are outlined in Table 1. Modern programs employ additional mathematical techniques to accelerate the convergence of the orbitals.
Table 1: SCF Procedure for the Hartree-Fock Method
|
(1) Initial guess for the orbitals
|
(2) Use the orbitals to construct the J and K terms
|
(3) Solve the effective Hamiltonian for an updated set of orbitals
|
(4) Repeat steps (2) and (3) until convergence
|
Example
As an example, we apply the Hartree-Fock method, implemented in the Quantum Chemistry Toolbox in Maple, to computing the molecular orbitals and their energies for the benzene molecule. First, we import a geometry for the molecule benzene,
| > |
benzene := QuantumChemistry:-MolecularGeometry("benzene"); |
whose 3D ball-and-stick structure is
| > |
QuantumChemistry:-PlotMolecule(benzene); |
We perform the Hartree-Fock calculation in a finite atomic-orbital basis set, known as the correlation-consistent polarized double-zeta basis set (cc-pVDZ), which returns a Maple table assigned to the variable data. We use the colon rather semicolon than the to terminate the command to suppress printing of the table for brevity.
| > |
data := QuantumChemistry:-HartreeFock(benzene, basis="cc-pVDZ"): |
The variable data contains the total energy of benzene's ground state in the Hartree-Fock approximation
![Typesetting:-mprintslash([energy := -230.722043853874], [HFloat(-230.7220438538739)])](images/WhatIsHartreeFock_30.gif) |
(4.2) |
The energy is given in atomic units of energy which are known as hartrees in honor of Daniel Hartree. The molecular orbital energies are
| > |
mo_energies := data[mo_energy]; |
![_rtable[36893490064929480564];](images/WhatIsHartreeFock_31.gif) |
(4.3) |
In particular, the highest-occupied molecular orbital (HOMO) and lowest-unoccupied molecular orbital (LUMO) energies are
| > |
homo_energy := data[mo_energy][42/2];
lumo_energy := data[mo_energy][42/2+1]; |
![Typesetting:-mprintslash([homo_energy := -.333619390396818], [HFloat(-0.3336193903968183)])](images/WhatIsHartreeFock_32.gif) |
![Typesetting:-mprintslash([lumo_energy := .137191473609525], [HFloat(0.13719147360952466)])](images/WhatIsHartreeFock_33.gif) |
(4.4) |
From the HOMO and LUMO energies we can compute an estimate of the excitation energy, the energy required to excite benzene to its first-excited state
| > |
excitation_energy := lumo_energy-homo_energy; |
![Typesetting:-mprintslash([excitation_energy := .470810864006343], [HFloat(0.470810864006343)])](images/WhatIsHartreeFock_34.gif) |
(4.5) |
or converting from hartrees to electron volts (eV), we have
| > |
excitation_energy := convert(excitation_energy, units, hartree, eV); |
![Typesetting:-mprintslash([excitation_energy := 12.8114161623876], [HFloat(12.811416162387593)])](images/WhatIsHartreeFock_35.gif) |
(4.6) |
or converting from eV to kcal/mol, we have
| > |
excitation_energy := convert(excitation_energy, units, eV, kcal)*evalf(ScientificConstants:-Constant(N[A])); |
![Typesetting:-mprintslash([excitation_energy := 295.438277526591], [HFloat(295.4382775265913)])](images/WhatIsHartreeFock_36.gif) |
(4.7) |
The electron density of the HOMO from the Hartree-Fock calculation is
| > |
QuantumChemistry:-DensityPlot3D(benzene, data, basis="cc-pVDZ", orbitalindex=42/2, gridspacing=0.001, maximumpoints=400000); |
We observe the nodal plane between the upper 3 carbon atoms and the lower 3 carbon atoms. Similarly, the electron density of the LUMO from the Hartree-Fock calculation is
| > |
QuantumChemistry:-DensityPlot3D(benzene, data, basis="cc-pVDZ", orbitalindex=42/2+1, gridspacing=0.001, maximumpoints=400000); |
Selected References
1. D. R. Hartree, Math. Proc. Camb. Phil. Soc. 24, 111-132 (1928). "The wave mechanics of an atom with a non-Coulomb central field. Part II. Some results and discussion"
2. J. C. Slater, Phys. Rev. 35, 210–211 (1930). "Note on Hartree's Method"
3. V. Fock, Z. Physik 61, 126-148 (1930). "Näherungsmethode zur lösung des quantenmechanischen mehrkörperproblems"
4. D. R. Hartree and W. Hartree, Proc. Royal Soc. Lond. A. 150, 9 (1935). "Self-consistent field, with exchange, for beryllium"
5. C. C. J. Roothaan, Rev. Mod. Phys. 23, 69–89 (1951). "New developments in molecular orbital theory"
6. A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory (Dover Books, New York, 1996).
7. Quantum Chemistry Toolbox in Maple (Maplesoft, Waterloo, 2023).
Written by David A. Mazziotti

![]()
![]() = En
= En ![]()
![]()
![]()
![]()
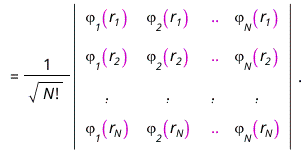
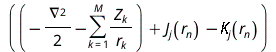
![]()
![]() = εn
= εn ![]()
![]()
![]()
![]()
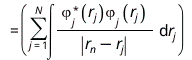
![]()
![]()
![]()
![]()

![]()
![]()

![_rtable[36893490064929480564];](images/WhatIsHartreeFock_31.gif)

