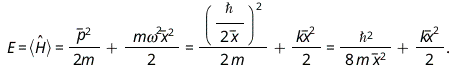What Is? 

For a quantum mechanical system, its zero-point energy is the lowest possible energy it may have. The state at which the system has a minimum energy is called its ground state. Heisenberg’s uncertainty principle states that, even at ground state, the system perpetually fluctuates. When we approximate a fluctuating, or “vibrating,” particle as a harmonic oscillator, we may mathematically demonstrate that the uncertainty principle dictates a positive zero-point energy , where is the ground state angular frequency. Given a system’s ground state wave function, we may compute the zero-point energy by solving the Schrödinger equation. In quantum field theory, zero-point energy refers to the lowest possible energy of a field, such as the electromagnetic field; the zero-point energy of the fabric of space is called vacuum energy, which is empirically verified by the Casimir effect. 

History 

In 1900, Max Planck published his pioneering hypothesis that energy is not continuously distributed but are quantized. Instead of a continuous, smooth curve, energy function is shaped by infinitesimal batches of energy (called "quanta") that cannot be further divided. This is analagous to how in calculus class we approximate a smoothly curved function as a sum of infinitesimally thin rectangles, except Planck stated that, for energy, our approximation is closer to reality than the smooth curve. He assumed that a hypothetical oscillator in a well containing black-body radiation could only change its energy in the minimal increment , where is its ordinary frequency. Under this hypothesis Planck offered a successful solution to the "ultraviolet catastrophe," a problem classical theory failed to solve. Eleven years later, he derived that, at zero temperature, the energy of an oscillator does not become zero but equals , thereby introducing the term “zero-point energy.” This theory would be supported by several experimental results. In 1925 R.S. Mulliken studied the vibrational band spectra of boron monoxide and showed plausibility of the existence of ; in 1927, R.W. James and E.M. Firth’s X-ray diffraction experiments detected zero-point motion. Half a year after Mulliken’s experiment, Werner Heisenberg published what many consider as the commencing article on quantum mechanics, in which he demonstrated the uncertainty principle and then derived therefrom that the zero-point energy of a harmonic oscillator is . In 1948, using the concept of zero-point energy, Hendrik Casimir derived the retardation due to the finite speed of light on the London–van der Waals force. His derivation would be experimentally confirmed in 1997. With the auspice of quantum field theory, Edward Tyron in 1973 hypothesized that the universe may be a vacuum fluctuation where negative gravitational potential is balanced by a positive “vacuum energy”; since the end of the 20th century, NASA scientists have looked into the possibility of harnessing the vacuum energy. 

Details 

For a system with smooth potential curve, we can approximate the potential to that of a harmonic oscillator. The Hamiltonian operator of the one-dimensional harmonic oscillator 

where is the displacement, the momentum, the mass, the force constant of the oscillator. Given Heisenberg's uncertainty principle 

where and are uncertainties, i.e. standard deviations, of displacement and momentum, respectively, we can assume that, at ground state, , , and so .

The zero-point energy is the expectation value of the Hamiltonian 

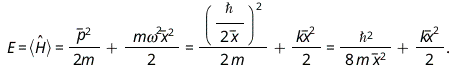
To obtain the minimum argument , we can compute the derivative of and set it to zero, we can thus obtain a relationship for minimum argument of : 

Plugging it back to the equation above, we  obtain 

where 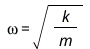and are the angular and ordinary frequencies of the harmonic oscillator, respectively. 

(3.1)

 

Example 

Equipped with the equation, we can calculate the zero-point energy of a system from its vibrational ground state. For instance, let us compute the zero-point energy of hydrogen gas molecule given its vibrational wavenumber. 

>

 

(4.1)

 

>

 

(4.2)

 

To achieve higher accuracy, we optimize its geometry with Hartree--Fock method. 

>

 

(4.3)

 

>

 

(4.4)

 

The first value we obtain is the ground state vibrational wavenumber . We can use this information to calculate . 

>

 

(4.5)

 

>

 

(4.6)

 

>

 

(4.7)

 

>

 

(4.8)

 

Convert the obtained ZPE of a single hydrogen molecule to ZPE per mole: 

>

 

(4.9)

 

Let us check our math: 

>

 

(4.10)

 

The Hartree--Fock method predicts the ZPE to be , which agrees with our calculation obtained from the uncertainty principle for the quantum harmonic oscillator model. But the experimental value for zero-point energy of hydrogen molecule is 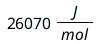, and so our we overpredicted by 25.29%. This is in part because by using only the uncertainty principle (or Hartree-Fock method) we neglected electronic correlation, which stabilizes the system and so yields a lower zero-point energy. In addition, the shape of the true potential well of the hydrogen molecule is not exactly that of a harmonic oscillator but closer to that of the Morse potential, whereof the energy is lower than their harmonic-oscillator counterparts. Nonetheless, we are confident to confirm that the lowest possible energy of a quantum system is indeed above zero. 

Selected References 

1. Follow-up: What is the 'zero-point energy' (or 'vacuum energy') in quantum physics? is it really possible that we could harness this energy? https://www.scientificamerican.com/article/follow-up-what-is-the-zer/ (accessed Jan 31,  2023).
2. Boyer, T. H. Quantum Zero-Point Energy and Long-Range Forces. Annals of Physics 1970, 56, 474–503.  

3. Irikura, K. K. Experimental Vibrational Zero-Point Energies: Diatomic Molecules. Journal of Physical and Chemical Reference Data 2007, 36, 389–397.
4. Levitt, L. S. Derivation of the Zero-Point Energy from the Uncertainty Principle. Journal of Chemical Education 1962, 39, 520.
5. Millis, M. G. Challenge to Create the Space Drive. Journal of Propulsion and Power 1997, 13, 577–582.
6. Planck's Half-Quanta: A History of the Concept of Zero-Point Energy. The Golden Age of Theoretical Physics 2001, 56–93.  

7. Vinh, N. G.; Ngu, M. V.; Lan, N. T.; Thanh, L. T.; Dung, N. T.; Viet, N. A. Some Applications Using the Connection betweenq-Deformed Harmonic Oscillator and Symmetric and Asymmetric Potentials. Journal of Physics: Conference Series 2017, 865, 012006.  

Written by Thomas Qu