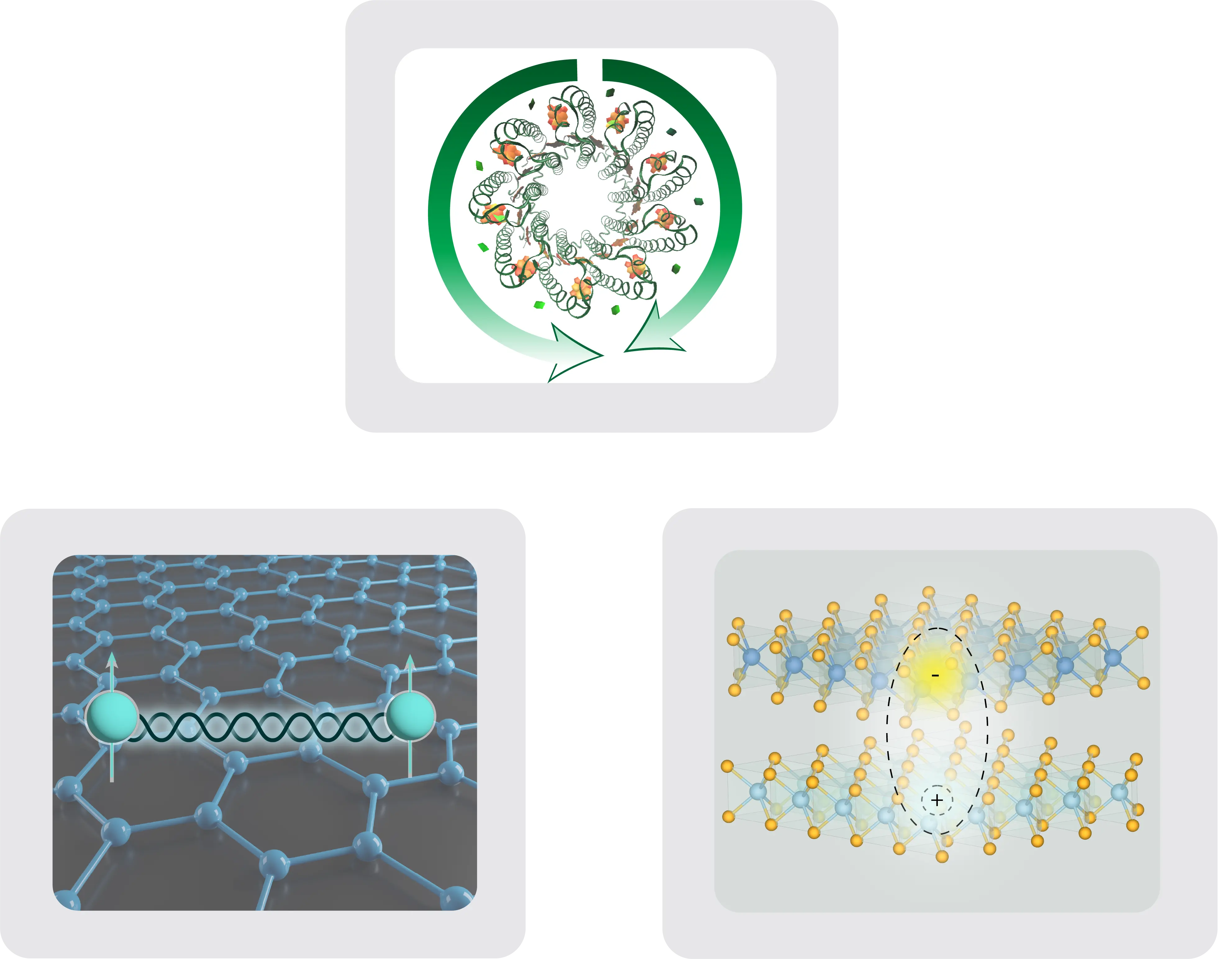
Reduced Density Matrix Theory and Strong Correlation

The many-electron problem in chemistry and physics is challenging because the wave function, containing much more information than is needed for physical properties, scales exponentially with system size. Our group develops methods based on reduced density matrices (RDMs), which capture the chemistry of many-electron systems with dramatically reduced computational cost. We have pioneered the development and practical implementation of N-representability conditions, which ensure that a two-electron RDM (2-RDM) corresponds to a physically valid N-electron quantum state. Two general methodologies developed by our group include: (1) the variational 2-RDM method, in which the energy is minimized directly with respect to the 2-RDM subject to these constraints, and (2) the contracted Schrödinger equation (CSE) method, in which we solve a projection of the Schrödinger equation onto the space of two electrons. Recent advances have enabled cutting-edge applications to complex inorganic molecules, including amorphous coordination polymers studied in collaboration with experimental groups.

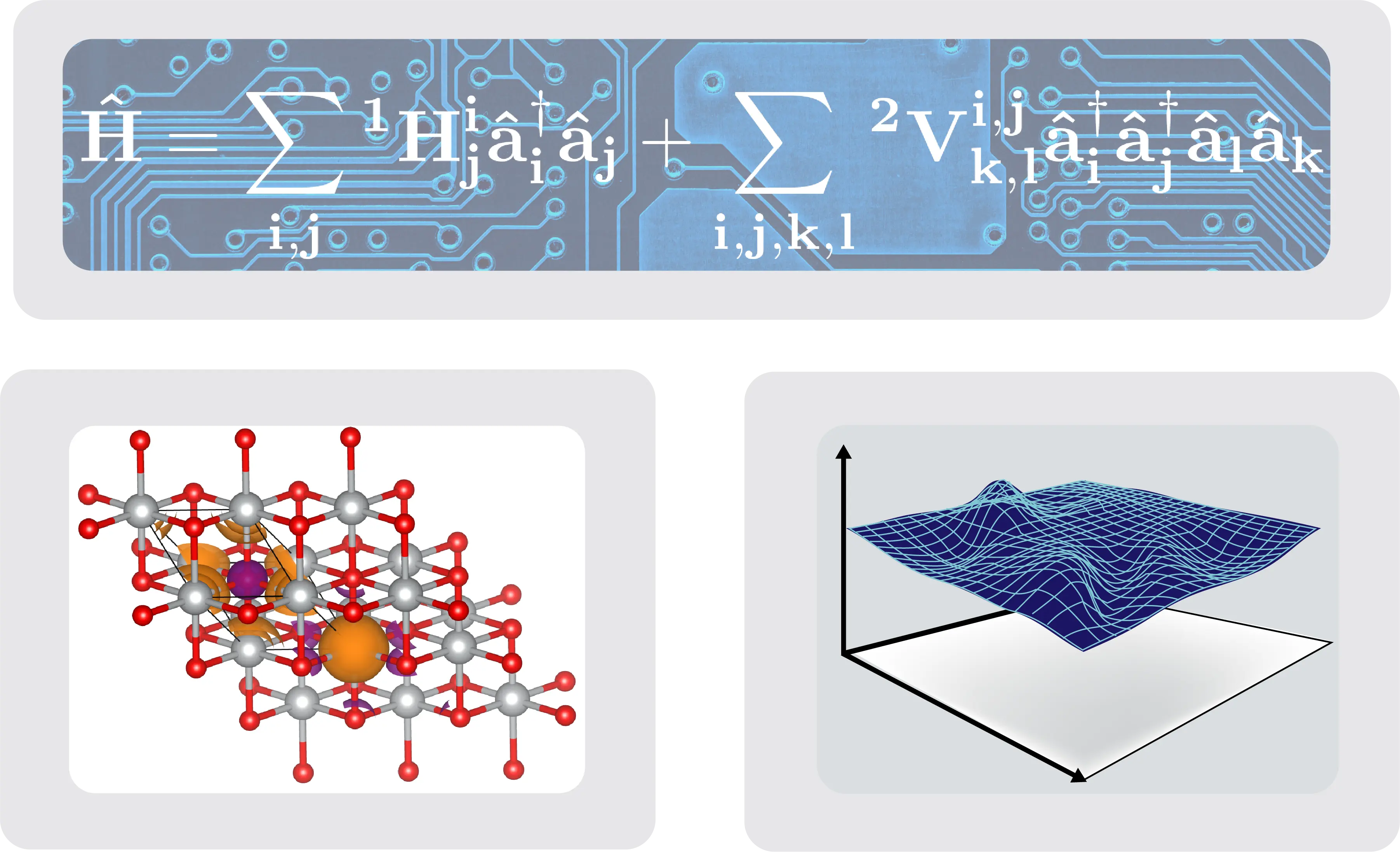
Correlated Generalizations of Density Functional Theory

A major challenge for density functional theory (DFT) is its failure to treat static correlation, yielding errors in predicted charges, band gaps, van der Waals forces, and reaction barriers. We recently combined one- and two-electron reduced density matrix (1- and 2-RDM) theories with DFT to obtain a universal O(N³) generalization of DFT capable of capturing static correlation. This new framework retains the computational efficiency of DFT while extending its applicability to strongly correlated systems, opening new frontiers in the prediction of large, statically correlated molecules and materials. Initial applications show significant improvements in atomization energy benchmarks, the barrier to rotation in ethene, and the singlet–triplet gap in the linear acenes.

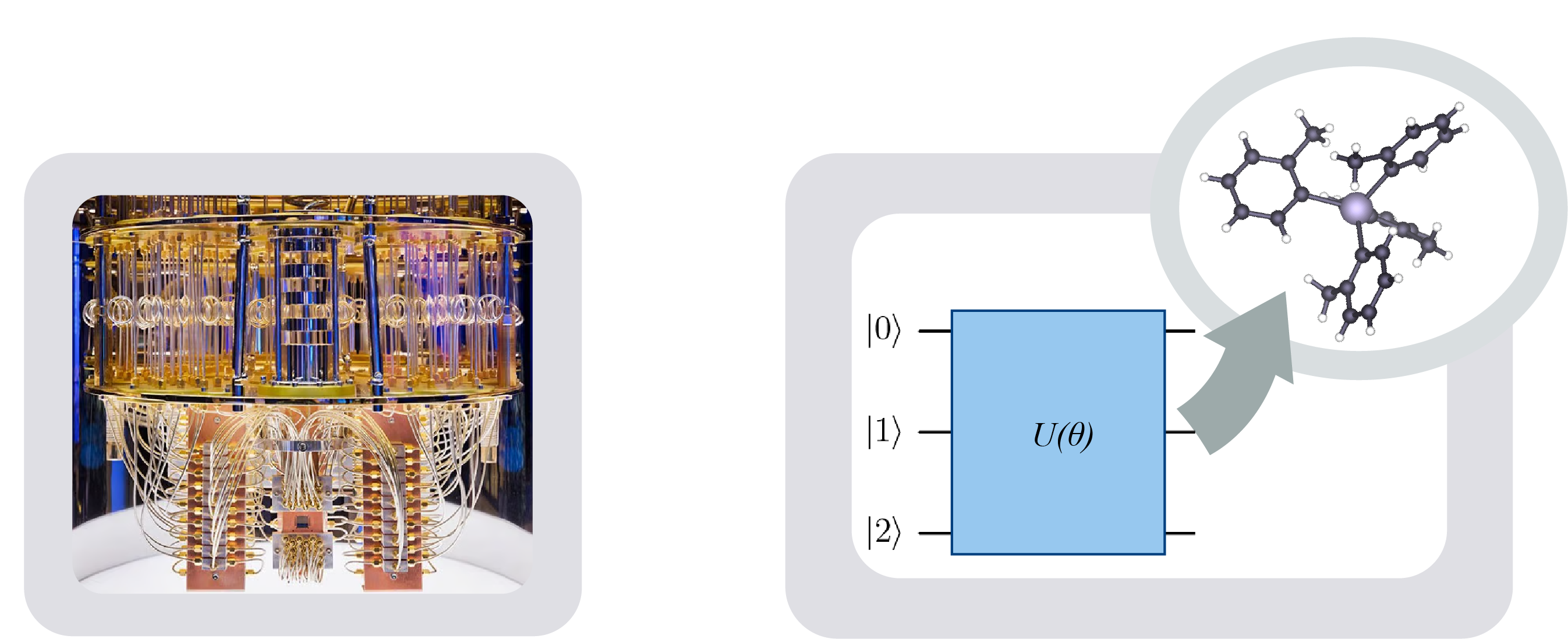
Quantum Algorithms for Molecular Simulation

Quantum computing offers the potential to transform molecular simulation by solving quantum many-body problems with improved accuracy and scaling. Our group develops quantum algorithms that leverage reduced density matrices (RDMs) to make this promise more tractable on current and near-term devices. We introduced the contracted quantum eigensolver (CQE), a hybrid quantum-classical algorithm that variationally optimizes the 2-RDM rather than the wave function, enabling efficient treatment of both ground and excited states. We also develop constrained shadow tomography, which reduces the number of measurements required on quantum hardware by incorporating physical symmetries and quantum constraints. These methods and further advances will help to realize the goal of accurate quantum simulations on current and future quantum computers. We have used quantum hardware to experimentally verify a generalization of the Pauli exclusion principle and to realize exciton condensation, demonstrating the potential of quantum devices to probe fundamental many-body phenomena.

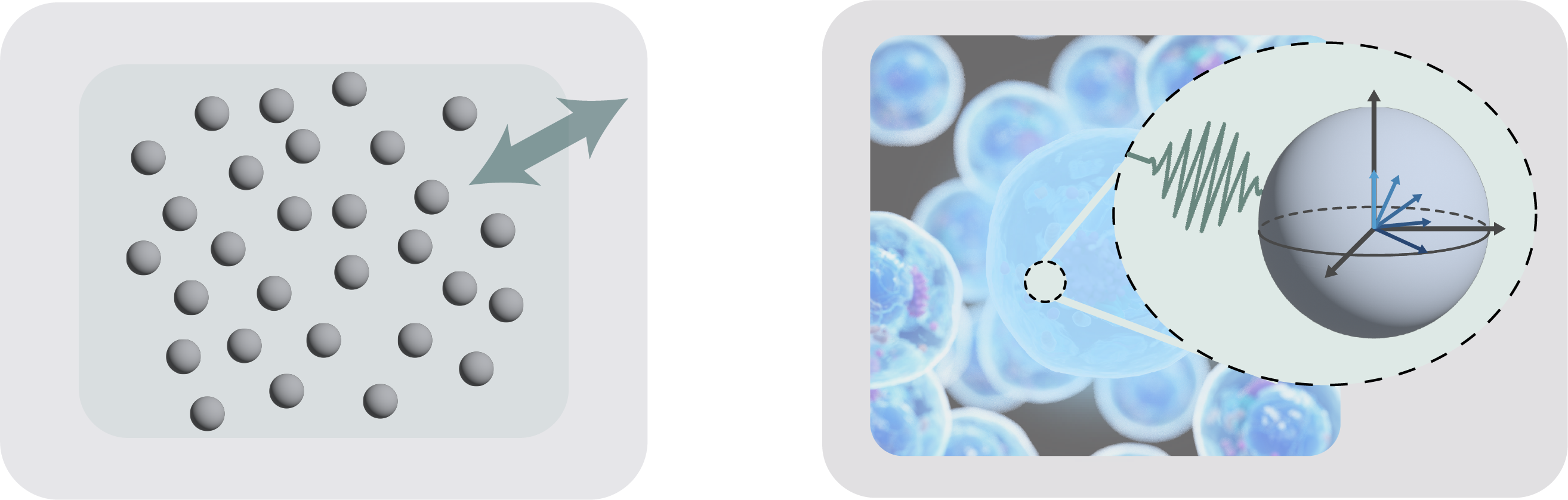
Quantum Entanglement in Biology and Materials

We investigate how quantum entanglement and coherence govern transport, energy flow, and emergent phenomena in biological systems and quantum materials. Our group has developed reduced density matrix–based entanglement witnesses to detect condensation phenomena—including exciton condensation and superconductivity—directly from electronic structure. These tools provide molecular-level insight into the origins of long-range quantum order in complex systems. Recently, we have shown that partial exciton condensation, a form of quantum coherence characterized by off-diagonal long-range order (ODLRO), can enhance classical energy transfer in light-harvesting complexes such as LH2 and FMO. These findings deepen our understanding of quantum biology and offer design principles for synthetic materials that exploit quantum correlations to achieve efficient energy transport. We are also exploring how entanglement can contribute to enhanced sensitivity in molecular sensors, with potential applications spanning materials science, biology, and medicine.

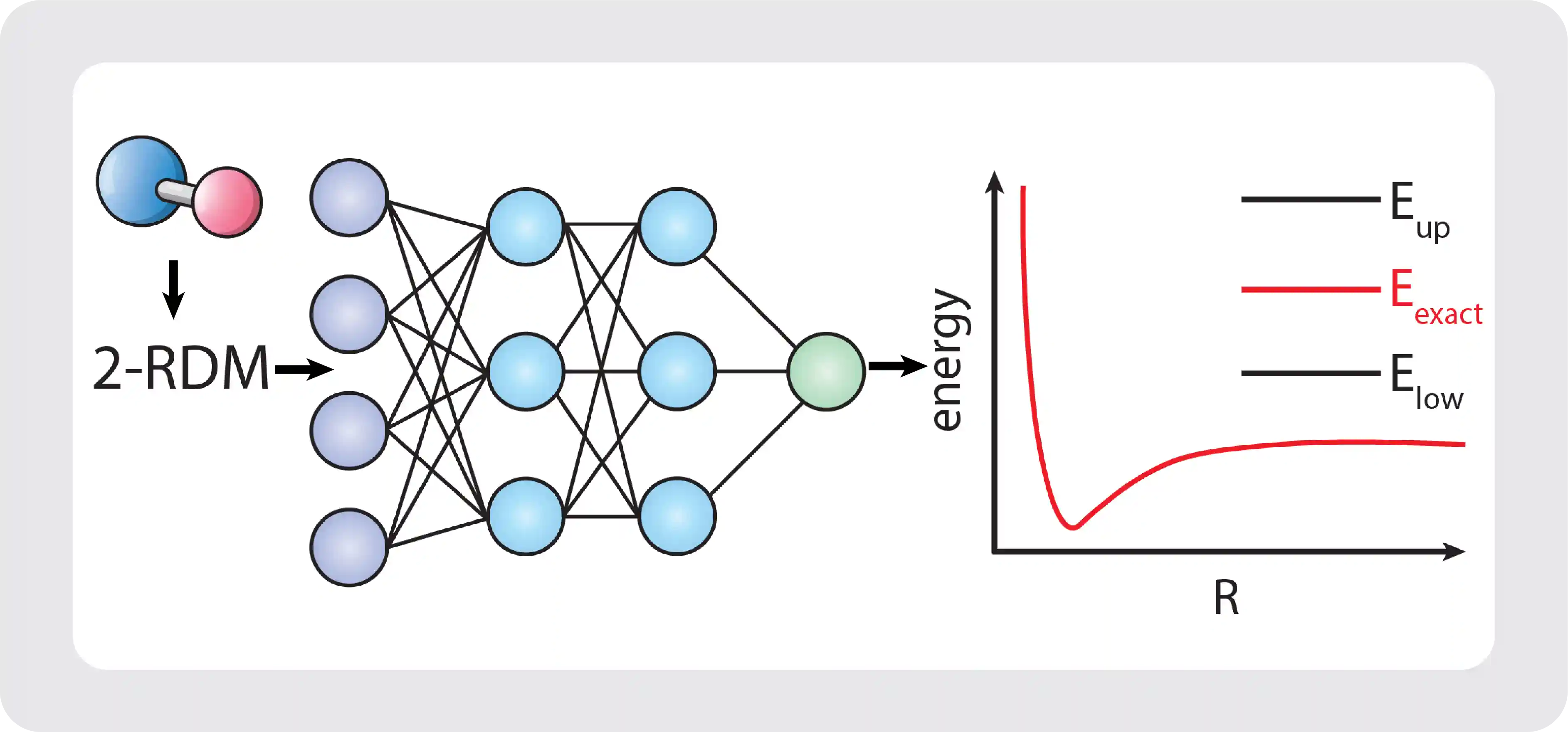
Machine Learning of Quantum Systems

We develop machine learning (ML) approaches that incorporate physical structure and constraints to address the quantum many-electron problem. In recent work, we introduced a convolutional neural network to learn geminal occupation distributions—the weights that express a many-electron system as a convex combination of two-electron wave functions—effectively reducing the many-electron problem to a two-electron one. We also developed a physics-informed ML algorithm that predicts two-electron reduced density matrices (2-RDMs) and their energies using only a small amount of molecular training data. By incorporating N-representability conditions and energy bounds, this approach captures both dynamic and static correlation without relying on steeply scaling wave function methods or empirical functionals. In addition, we have used reinforcement learning to accelerate the contracted quantum eigensolver (CQE) by identifying efficient wave function updates on quantum hardware. These developments provide a general framework for improving electronic structure and quantum simulation with interpretable, data-efficient machine learning.